/other
Mathematic calculations to cool coffee
How many ice cubes do you need to quickly cool down a hot beverage to its perfect drinking temperature?
Lets use physics to find the exact number of ice cubes to drop into a scalding hot cup of coffee or tea to make it the perfect temperature.
The beverage
The hot beverage must lose a certain amount of energy in order to decrease its temperature to a warm temperature. The energy of heat loss is given by a difference of temperature. The equation is
$$Q_{beverage} = c_{water} \times m_{beverage} \times \Delta T_{beverage}$$
The specific heat of water, $c_{water}$ is 4.2 $J / g / °C$. The mass of a typical cup of coffee or tea, $m_{beverage}$ is typically around 480 grams. The change in temperature, $\Delta T_{beverage}$, is the change between the initial brewing temperature and the final drinking temperature.
$$Q_{beverage} = c_{water} \times m_{beverage} \times (T_{i}-T_{f})$$
The ice
Ice melts by absorbing heat, or energy. The heat absorbed by ice is given by
$$ Q_{ice} = m_{ice} \times Q_{fusion}$$
where $Q_{fusion}$ is the enthalpy of fusion for ice, which is 334 $J/g$. Enthalpy of fusion is simply the amount of energy that will be needed to transform ice into cold water.
Once the ice changes into cold water, it will begin to warm up, by absorbing heat from the beverage. As before, the water will absorb according to the equation
$$Q_{ice-water} = c_{water} \times m_{ice} \times \Delta T_{ice}$$
In this case, the change in temperature, $\Delta T_{ice}$, is simply the final temperature, $T_{f}$, since ice has a temperature of 0°C.
$$Q_{ice-water} = c_{water} \times m_{ice} \times T_{f}$$
The beverage + ice
When we reach equilibrium, it means that the total energy lost by the beverage equals the sum of the energy of the ice and the cold water (once the ice has transformed), $Q_{beverage}= Q_{ice-water} + Q_{ice}$. When we plug in the equations above we get
$$ c_{water} \times m_{beverage} \times (T_{i}-T_{f}) = m_{ice} \times Q_{fusion} \\ + c_{water} \times m_{ice} \times T_{i} $$The only unknown is the mass of the ice, $m_{ice}$, which we can solve for to get
$$ m_{ice} = \frac{c_{water} \times m_{beverage} \times (T_{i}-T_{f})}{Q_{fusion} + c_{water} \times T_{i}} $$
How many ice cubes do you need?
Coffee is initially at a temperature of 85°C. Tea has a similar high, undrinkable, temperature. The perfect drinking temperature is 50°C. Given a typical cup of tea is about 480 grams, you need about 4 regular sized ice cubes. (A regular ice cube from a ice tray is about 30 g).
How fast does an ice cube melt?
How much times does it take for the ice to melt? There are several modes of heat transfer - conduction, convection, radiation. It turns out that ice is pretty well described by mainly the convection heat transfer. This is described by Fourier’s law of thermal conduction:
$$ \dot{Q}_{melt} = k A \frac{d T}{d x} $$
where $\dot{Q}_{melt}$ is the heat flux and $k$ is the thermal conductivity. For water, the thermal conductivity is 0.591 $W / m / K$.
Ice cube area
The area of the ice cube can be approximated by a cube of the same mass. That is,
$$ A = 6 \times (m_{ice})^{2/3} / 100^2 $$
where the mass of each one is $m_{ice}$ and the $100^2$ is for converting $cm^2$ to $m^2$. Though, really the surface area of the ice cubes might depends on time (the ice cube grows smaller).
Temperature gradient
The gradient of the temperature is between the surface of the ice and the rest of the hot water. Though this gradient can be pretty complicated (the heat diffusion occurs), we can approximate from the literature. Here is an infrared image of ice melting at room temperature1:

As you can see, the ice-air boundary is typically 0.002 meters, so we can approximate the ice water-boundary as $dx = 0.002$. The temperature difference is just the difference between the water and the ice, which is at 0, so $dT = T_{i}$.
How long does it take to melt?
Finally, then to get the time we can just use the equation from before and divide: $$ t_{melt} = Q_{ice} / \dot{Q}_{melt} $$
so that
$$ t_{melt} = \frac{m_{ice} \times H_{fusion}}{k \times T_{i} \times 6 \times m_{ice}^{2/3} / 100^2 / dx } $$
which is measured in seconds.
A typical ice cube weighs about 30 grams and a typical initial temperature for heated water is about 85°C. So a typical ice cube melts in about 70 seconds.
Theory versus Experiment
I hooked up an Arduino to a DS18B20 temperature probe and measured the change in temperature over time of 480 grams of water, with (red line) and without (blue line) ice.
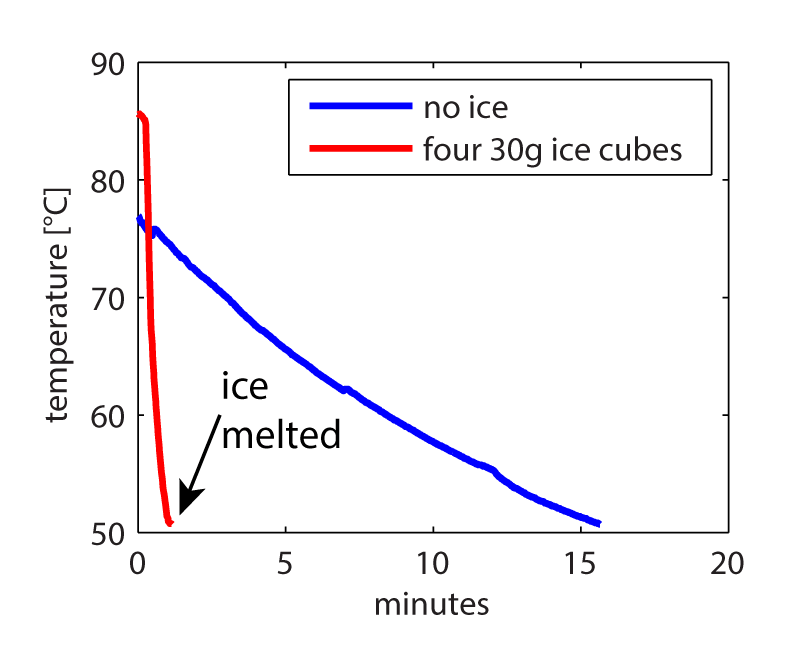
The ice melted in about 65 seconds and brought the temperature down to 50.8°C. This is in good agreement to the theoretical time to melt of 70 seconds and the theoretical final temperature of 50°C.
In comparison, the water without out that started at about 77°C, without ice, took over 15 minutes to get to the same temperature!
References
- Badarch, Ayurzana. (2017). Application of macro and mesoscopic numerical models to hydraulic problems with solid substances. 10.13140/RG.2.2.27837.36325. [return]